Wir planen und entwickeln mit Ihnen die richtige Lösung für Ihre Anforderungen. Wir erstellen Gesamtlösungen, die Ihre Bedürfnisse an Digitalisierung durch künstliche Intelligenz in Entwicklung und Produktion perfekt erfüllen.
Unsere erfahrenen ExpertInnen setzen für Sie KI-basierte Lösungen für Anwendungen wie predictive Quality, predictive Maintenance, Anomalieerkennung, Produktionsoptimierung und Produktentwicklung um.
Als Teil der Terra Quantum AG machen wir nun auch für klassische Anwendungen den Sprung zum Quantum Computing möglich, mit Quantum Assisted Machine Learning und Optimierung. Quantum is Now.
Wir planen und entwickeln mit Ihnen die richtige Lösung für Ihre Anforderungen. Wir erstellen Gesamtlösungen, die Ihre Bedürfnisse an Digitalisierung durch künstliche Intelligenz in Entwicklung und Produktion perfekt erfüllen.
Unsere erfahrenen ExpertInnen setzen für Sie KI-basierte Lösungen für Anwendungen wie predictive Quality, predictive Maintenance, Anomalieerkennung, Produktionsoptimierung und Produktentwicklung um.
Als Teil der Terra Quantum AG machen wir nun auch für klassische Anwendungen den Sprung zum Quantum Computing möglich, mit Quantum Assisted Machine Learning und Optimierung. Quantum is Now.
Industrien
Alle Anwendungen, bei denen Produkte oder Prozesse optimiert werden sollen, sind für unsere Methoden geeignet. Es können Daten aus Experimenten, Simulationen oder direkt aus dem Prozess verwendet werden. Basierend auf diesen Daten optimieren wir das Produkt oder den Prozess.
Alle Anwendungen, bei denen Produkte oder Prozesse optimiert werden sollen, sind für unsere Methoden geeignet. Es können Daten aus Experimenten, Simulationen oder direkt aus dem Prozess verwendet werden. Basierend auf diesen Daten optimieren wir das Produkt oder den Prozess.
Software
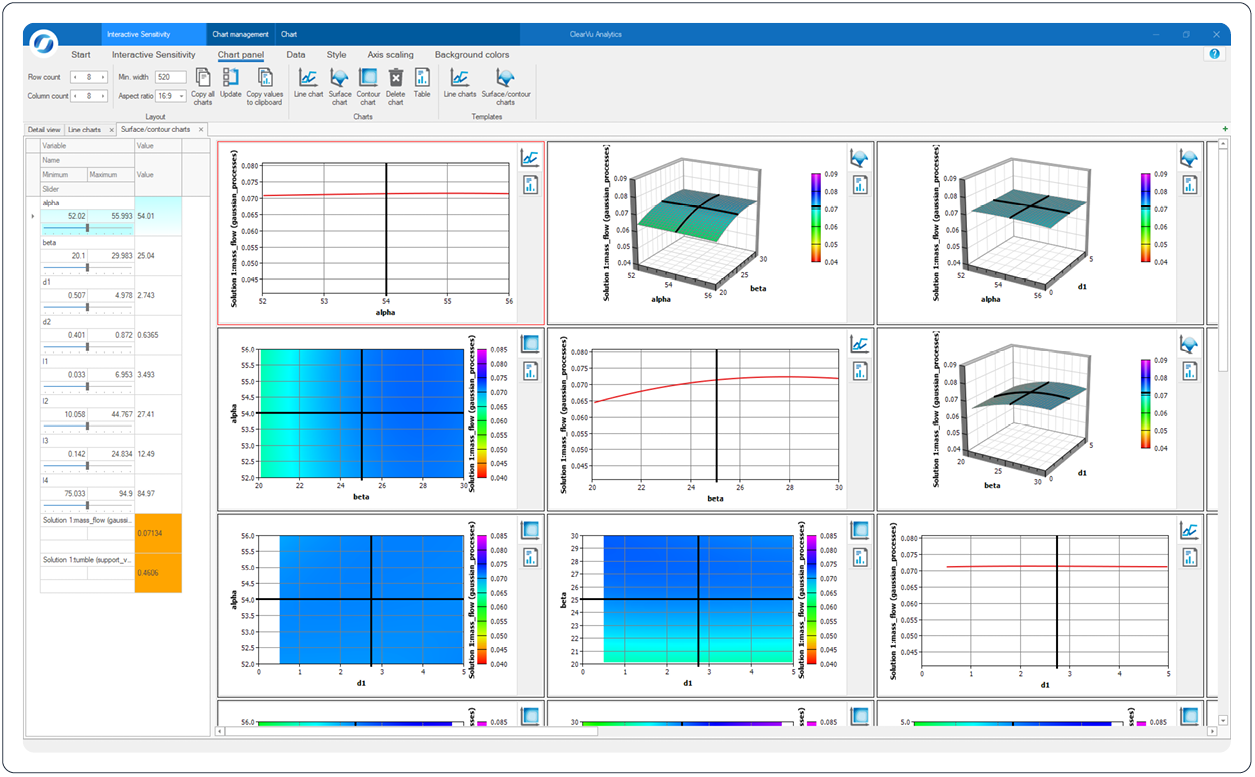
Zusätzlich zu unserer hauseigenen Software, entwickeln wir für Sie maßgeschneiderte Systeme nach Ihren individuellen Anforderungen. Dazu passen wir unsere Module an Ihre unternehmensspezifischen Voraussetzungen an und gestalten die Benutzeroberfläche nach Ihren Bedürfnissen. Darüber hinaus binden wir unsere Software an Ihre interne Datenbank an. Das fertige System wird in Ihre interne IT-Umgebung und den bestehenden Produktionsprozess integriert.
Zusätzlich zu unserer hauseigenen Software, entwickeln wir für Sie maßgeschneiderte Systeme nach Ihren individuellen Anforderungen. Dazu passen wir unsere Module an Ihre unternehmensspezifischen Voraussetzungen an und gestalten die Benutzeroberfläche nach Ihren Bedürfnissen. Darüber hinaus binden wir unsere Software an Ihre interne Datenbank an. Das fertige System wird in Ihre interne IT-Umgebung und den bestehenden Produktionsprozess integriert.
Software
Zusätzlich zu unserer hauseigenen Software, entwickeln wir für Sie maßgeschneiderte Systeme nach Ihren individuellen Anforderungen. Dazu passen wir unsere Module an Ihre unternehmensspezifischen Voraussetzungen an und gestalten die Benutzeroberfläche nach Ihren Bedürfnissen. Darüber hinaus binden wir unsere Software an Ihre interne Datenbank an. Das fertige System wird in Ihre interne IT-Umgebung und den bestehenden Produktionsprozess integriert.

ClearVu Solution Spaces (CVSS) unterstützt Sie bei der Auslegung von Systemen und Komponenten in der Automobilindustrie. Dabei sind viele Restriktionen einzuhalten und CVSS stellt eine optimale Flexibilität für die Identifikation von Auslegungsvarianten zur Verfügung.
Das Excel Add-In stellt Ihnen mit wenigen Klicks Automated Machine Learning direkt in Excel zur Verfügung, um Prognosemodelle für Ihre Datensätze zu erzeugen. Das resultierende Prognosemodell kann als Zellfunktion direkt für Prognosen verwendet und das Modell selbst kann analysiert und visualisiert werden.
Das ClearVu Python Package stellt die Funktionalität von ClearVu Analytics in Python zur Verfügung. Damit ist Automated Machine Learning ohne weiteren Einarbeitungsaufwand in Python benutzbar – schnell, automatisch und leistungsfähig.
Auszug aus unserer Referenzliste
_
BMW Group
_
Mercedes-Benz AG
_
Dr. Ing. h.c. F.
Porsche AG
_
Honda Research
Institute Europe GmbH
_
Hyundai Motor Company
_
Beiersdorf AG
_
IOI Oleo GmbH
_
Chemetall GmbH
_
ThyssenKrupp
Industrial Solutions AG
_
Covestro AG
_
3M Deutschland GmbH
_
Johnson & Johnson
Deutschland
Testimonials
Kontakt
So erreichen Sie uns
Telefon
0231 97 00 340
Adresse
Joseph-von-Fraunhofer-Straße 20,
44227 Dortmund
Kontakt
So erreichen Sie uns
Telefon
0231 97 00 340
Adresse
Joseph-von-Fraunhofer-Straße 20,
44227 Dortmund














